5. Manipulability analysis¶
For this project, we also looked at the manipulability of the voting rules we introduced in the previous notebook. More precisely, we wanted to see if using ordinal extensions with our voting rules would lower the degree of manipulability.
That’s what we are going to see in this notebook, using the case of one of my favorite rules : SVDNash.
We analysed two kinds of manipulation :
- Single-voter manipulation
- Coalition trivial manipulation
I will explain these different manipulations in their respective sections.
[1]:
import numpy as np
import embedded_voting as ev
import matplotlib.pyplot as plt
np.random.seed(420)
First of all, we create a random profile with three groups of voter of the same size.
[2]:
n_voters = 50
n_candidates = 4
n_dim = 3
embeddingsGenerator = ev.EmbeddingsGeneratorPolarized(n_voters, n_dim)
ratingsGenerator = ev.RatingsFromEmbeddingsCorrelated(coherence=0.2, n_dim = n_dim, n_candidates = n_candidates)
embeddings = embeddingsGenerator(polarisation=0.4)
ratings = ratingsGenerator(embeddings)
embeddings.plot_candidates(ratings)
Single-voter manipulation¶
The single-voter manipulation is easy to understand.
Let’s say the winner of an election is candidate \(c_{w}\) and some voter \(v_i\) prefers candidate \(c_j\) to \(c_w\) (i.e. \(c_j >_i c_w\)). Then, \(v_i\) can manipulate the election by putting \(c_j\) first (even if it’s not his favorite candidate) and \(c_w\) last. More generally, if \(v_i\) can change his preferences so that \(c_j\) becomes the winner instead of \(c_w\), then \(v_i\) can manipulate the election for \(c_j\).
The questions we want to ask :
- What proportion of the population can manipulate the election?
- What is the average welfare obtained after manipulation of the election by a voter?
- What is the worst welfare obtained after manipulation of the election by a voter?
No extensions¶
Let’s create an election using the rule SVDNash. The winner is candidate \(c_4\).
[3]:
election = ev.RuleSVDNash()(ratings, embeddings)
print("Winner : ", election.winner_)
print("Ranking : ", election.ranking_)
print("Welfare : ", election.welfare_)
Winner : 3
Ranking : [3, 1, 0, 2]
Welfare : [0.24843681867948134, 0.7504122119950717, 0.0, 1.0]
With the class SingleVoterManipulation, I can answer the different questions about the manipulability.
To do so, when \(v_i\) manipulates as explained above, we only set the score of the candidate \(c_j\) to \(1\) and every other score is set to \(0\). It will work for every monotonic rule (which is the case of every rule we introduced).
For instance, in our election, a lot of the voters can manipulate the election, and the worst welfare that can be attained is the welfare of candidate \(c_1\), which is ranked second.
[4]:
manipulation = ev.Manipulation(ratings, embeddings, election)
print("Is manipulable : ", manipulation.is_manipulable_)
print("Proportion of manipulators : ", manipulation.prop_manipulator_)
print("Average welfare after manipulation : ", manipulation.avg_welfare_)
print("Worst welfare after manipulation : ", manipulation.worst_welfare_)
Is manipulable : False
Proportion of manipulators : 0.0
Average welfare after manipulation : 1.0
Worst welfare after manipulation : 1.0
Extensions¶
For ordinal extension (using rankings), we cannot use the above class, because if we set the score of every candidate to \(0\), we cannot rank the candidates anymore (they have the same score).
In the general case, we need to test every possible ranking for each voter. However, for some extension (borda, k-approval, instant runoff), we implemented faster algorithms for this.
For instance, with the Borda extension :
[5]:
ordinal_election = ev.RulePositionalBorda(n_candidates, rule=ev.RuleSVDNash())
ordinal_election(ratings, embeddings)
print("Winner : ", ordinal_election.winner_)
print("Ranking : ", ordinal_election.ranking_)
print("Welfare : ", ordinal_election.welfare_)
Winner : 3
Ranking : [3, 1, 0, 2]
Welfare : [0.33549316772419624, 0.7033412728596413, 0.0, 1.0]
Now, if we test the manipulability with SingleVoterManipulationExtension class, we reduce the number of manipulators
[6]:
ordinal_manipulation = ev.ManipulationOrdinal(ratings,
embeddings,
rule_positional=ordinal_election,
rule=election)
print("Is manipulable : ", ordinal_manipulation.is_manipulable_)
print("Proportion of manipulators : ", ordinal_manipulation.prop_manipulator_)
print("Average welfare after manipulation : ", ordinal_manipulation.avg_welfare_)
print("Worst welfare after manipulation : ", ordinal_manipulation.worst_welfare_)
Is manipulable : False
Proportion of manipulators : 0.0
Average welfare after manipulation : 1.0
Worst welfare after manipulation : 1.0
However, the above cell takes a lot of time (around \(15\) seconds). Using the specific class SingleVoterManipulationBorda, this computation time can be reduced to \(0.5\) seconds.
[7]:
borda_manipulation = ev.ManipulationOrdinalBorda(ratings,
embeddings,
rule=election)
print(borda_manipulation.extended_rule)
print("Is manipulable : ", borda_manipulation.is_manipulable_)
print("Proportion of manipulators : ", borda_manipulation.prop_manipulator_)
print("Average welfare after manipulation : ", borda_manipulation.avg_welfare_)
print("Worst welfare after manipulation : ", borda_manipulation.worst_welfare_)
<embedded_voting.rules.singlewinner_rules.rule_positional_borda.RulePositionalBorda object at 0x0000023B6FCD2E80>
Is manipulable : False
Proportion of manipulators : 0.0
Average welfare after manipulation : 1.0
Worst welfare after manipulation : 1.0
Using 3-Approval, we obtain less manipulators
[8]:
approval_manipulation = ev.ManipulationOrdinalKApproval(ratings, embeddings, k=3, rule=election)
print("Is manipulable : ", approval_manipulation.is_manipulable_)
print("Proportion of manipulators : ", approval_manipulation.prop_manipulator_)
print("Average welfare after manipulation : ", approval_manipulation.avg_welfare_)
print("Worst welfare after manipulation : ", approval_manipulation.worst_welfare_)
Is manipulable : False
Proportion of manipulators : 0.0
Average welfare after manipulation : 1.0
Worst welfare after manipulation : 1.0
Using Instant Runoff, the profile is not manipulable
[9]:
irv_manipulation = ev.ManipulationOrdinalIRV(ratings, embeddings, rule=election)
print("Is manipulable : ", irv_manipulation.is_manipulable_)
print("Proportion of manipulators : ", irv_manipulation.prop_manipulator_)
print("Average welfare after manipulation : ", irv_manipulation.avg_welfare_)
print("Worst welfare after manipulation : ", irv_manipulation.worst_welfare_)
Is manipulable : False
Proportion of manipulators : 0.0
Average welfare after manipulation : 1.0
Worst welfare after manipulation : 1.0
Coalition manipulation¶
The second kind of manipulation that is easy to compute and represent is the coalition manipulation. More specifically, is there a trivial manipulation by a coalition?
Let’s say that the winner of the election is the candidate \(c_w\) and let’s name \(V(j)\) the group of voters that prefer some candidate \(c_j\) to the winner \(c_w\):
Let’s say now that all these voters set \(c_j\) first and \(c_w\) last. Is \(c_j\) the new winner of the election ? If the answer is yes, then the profile is manipulable by a trivial coalition.
Obviously, if the profile is manipulable by a single voter, then it is also manipulable by a coalition.
No extensions¶
When we don’t use any extension, the profile is very manipulable. Indeed, every candidate can be elected after a trivial manipulation.
Consequently, the worst Nash welfare attainable is \(0\).
[10]:
manipulation = ev.ManipulationCoalition(ratings, embeddings, election)
print("Is manipulable : ", manipulation.is_manipulable_)
print("Worst welfare after manipulation : ", manipulation.worst_welfare_)
Is manipulable : False
Worst welfare after manipulation : 1.0
Extensions¶
However, it is a bit better when we use an ordinal extension. You can use the general class ManipulationCoalitionExtension or the specific classes for Borda, k-Approval and Instant runoff. However, they use the same algorithm.
Using Borda extension
[11]:
borda_extension = ev.RulePositionalBorda(n_candidates, rule=ev.RuleSVDNash())
borda_manipulation = ev.ManipulationCoalitionOrdinal(ratings, embeddings, borda_extension, election)
# manipulation = ev.ManipulationCoalitionBorda(profile, election)
print("Is manipulable : ", borda_manipulation.is_manipulable_)
print("Worst welfare after manipulation : ", borda_manipulation.worst_welfare_)
Is manipulable : True
Worst welfare after manipulation : 0.7504122119950696
Using 3-Approval
[12]:
kapp_manipulation = ev.ManipulationCoalitionOrdinalKApproval(ratings, embeddings, k=3, rule=election)
print("Is manipulable : ", kapp_manipulation.is_manipulable_)
print("Worst welfare after manipulation : ", kapp_manipulation.worst_welfare_)
Is manipulable : False
Worst welfare after manipulation : 1.0
Finally, with Instant Runoff voting
[13]:
irv_manipulation = ev.ManipulationCoalitionOrdinalIRV(ratings, embeddings, rule=election)
print("Is manipulable : ", irv_manipulation.is_manipulable_)
print("Worst welfare after manipulation : ", irv_manipulation.worst_welfare_)
Is manipulable : False
Worst welfare after manipulation : 1.0
Manipulation maps¶
However, we cannot really judge a rule or an extension on one example. That’s why we propose functions to show manipulation maps for some rule.
A map consists of an image of size \(s \times s\) such that each pixel represents one test. A dark pixel represents a \(0\) and a yellow pixel represents a \(1\).
Moreover, we use a parametric profile for each test and we vary the orthogonality and the correlation of the parametric profiles for each test: The more the pixel is on the right, the higher the correlation, and the more the pixel is on the top, the higher the orthogonality.
For each test, a new scores_matrix is randomly generated for the parametric profile.
No extensions¶
For instance, if we do not use extensions, we can see that the profiles are not very manipulable by single-voters, and when this is the case, the worst Nash welfare is high.
[14]:
manipulation = ev.Manipulation(ratings, embeddings, election)
res = manipulation.manipulation_map(map_size=25)
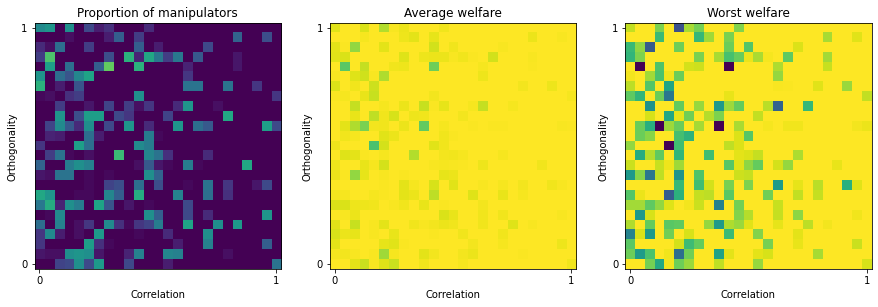
You can find the data used in the manipulation maps in the output of the function manipulation_map().
[15]:
res.keys()
[15]:
dict_keys(['manipulator', 'worst_welfare', 'avg_welfare'])
However, almost every profile is manipulable by trivial coalitions, and often the worst Nash welfare is \(0\):
[16]:
manipulation = ev.ManipulationCoalition(ratings, embeddings, election)
res = manipulation.manipulation_map(map_size=25)
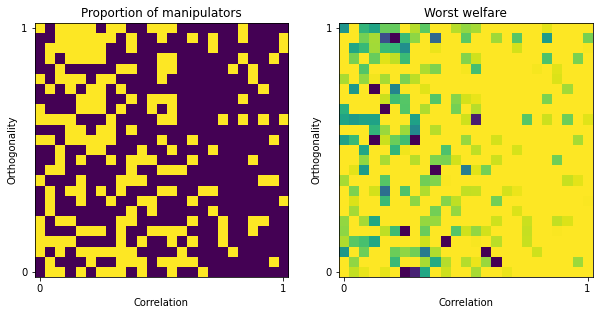
Again, the output of the function contains the data of the manipulation maps.
[17]:
res.keys()
[17]:
dict_keys(['manipulator', 'worst_welfare'])
Borda¶
With Borda, we improve a little bit the resistance to manipulation by coalition. However, we decrease the resistance to manipulation by a single-voter.
[18]:
borda_manipulation = ev.ManipulationOrdinalBorda(ratings, embeddings, rule=election)
res = borda_manipulation.manipulation_map(map_size=25)
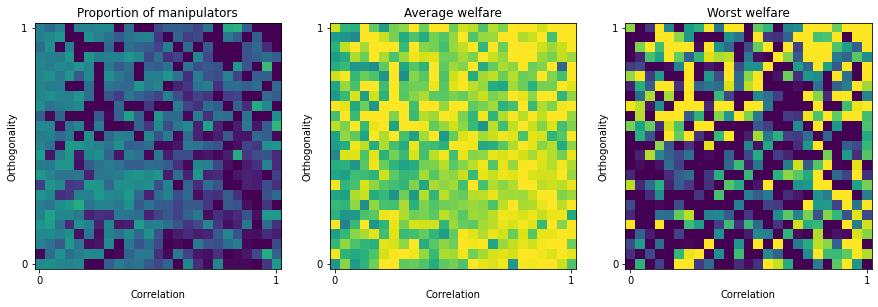
[19]:
borda_manipulation = ev.ManipulationCoalitionOrdinalBorda(ratings, embeddings, election)
res = borda_manipulation.manipulation_map(map_size=25)

IRV¶
With Instant Runoff, we increase by a lot the resistance to manipulation by coalition without altering the resistance to manipulation by a single voter.
[20]:
irv_manipulation = ev.ManipulationOrdinalIRV(ratings, embeddings, rule=election)
res = irv_manipulation.manipulation_map(map_size=25)
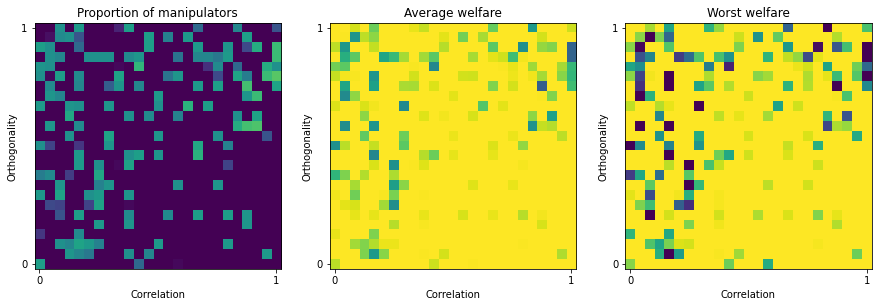
[21]:
irv_manipulation = ev.ManipulationCoalitionOrdinalIRV(ratings, embeddings, election)
res = irv_manipulation.manipulation_map(map_size=25)
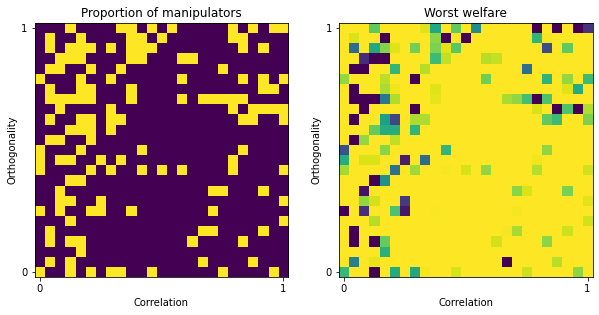
change map size¶
You can also plot more detailed manipulation maps by changing the map_size parameter.
[22]:
irv_manipulation = ev.ManipulationCoalitionOrdinalIRV(ratings, embeddings, election)
res = irv_manipulation.manipulation_map(map_size=100)
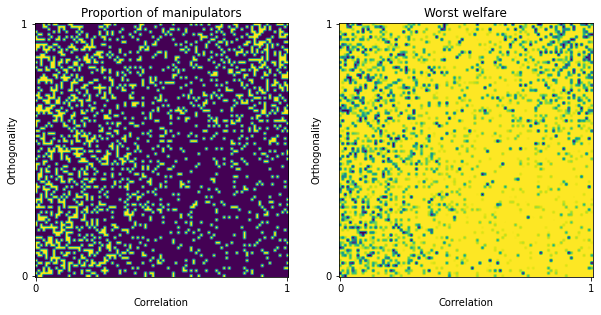
With particular scores matrix¶
In the previous plots, we changed the scores_matrix for each test (consequently, for each dot). You can modify that by specifying a matrix in the parameters of the function. It will use it for every test.
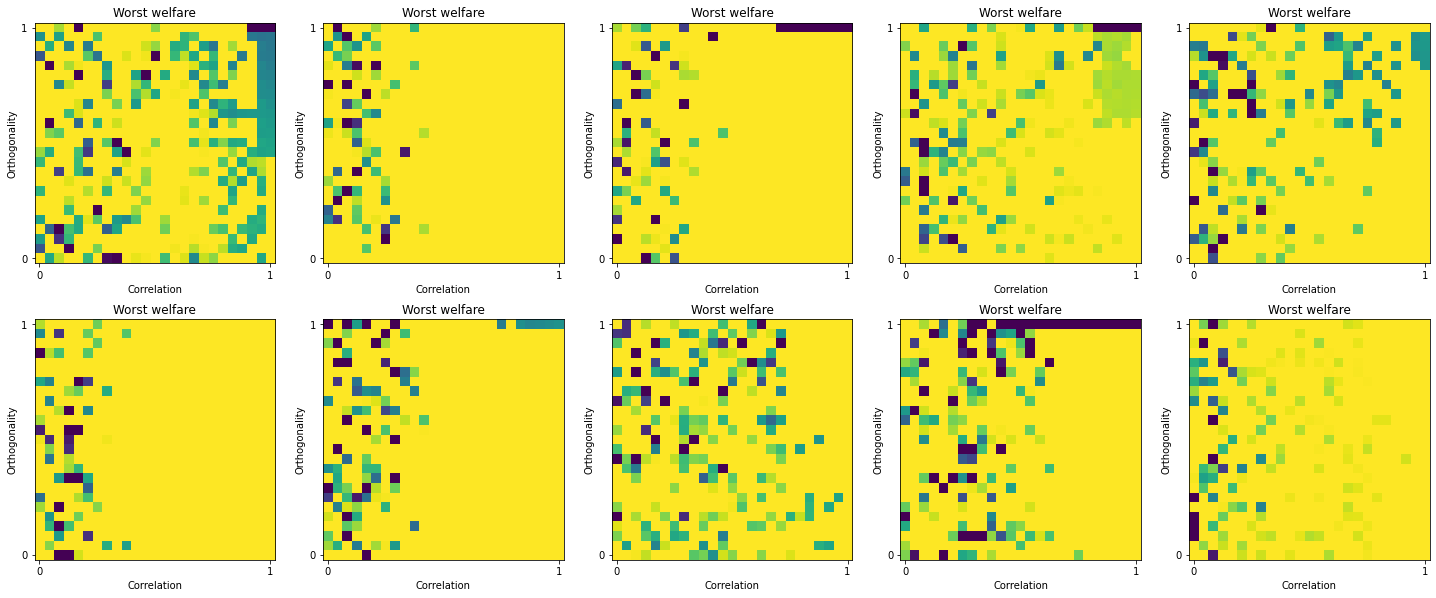
For instance, for Instant Runoff, you can see that the manipulation map heavily rely on this matrix: For some of them, there is a dark spot in the upper right corner (high correlation and high orthogonality).
[23]:
irv_manipulation = ev.ManipulationCoalitionOrdinalIRV(ratings, embeddings, election)
fig = plt.figure(figsize=(25, 10))
map_size = 25
for i in range(10):
res = irv_manipulation.manipulation_map(map_size=map_size, ratings_dim_candidate=np.random.rand(3, 4), show=False)
image = res['worst_welfare']
ev.create_map_plot(fig, image, [2, 5, i+1], "Worst welfare")